So you’ve set up your first client in Nutritics and you’re now on your way to faster, more efficient diet planning… but you’re wondering about the energy calculation formula.
We’re frequently asked questions about this during our calls with customers. What is an energy calculation formula? And which one is best for my clients? An accurate estimation of how much energy your client needs is critical for nutritional planning and assessment, so you’ll want to be sure you get this one right! The below guide will help with your decision process.
We have seven energy calculation formulas available in Nutritics:
- Henry Oxford 2005
- Institute of Medicine 2005
- Katch McArdle 1996
- Mifflin St. Jeor 1990
- Schofield 1985
- Cunningham 1980
- Harris-Benedict 1919
Put simply, these are all predictive equations used to estimate your client’s energy needs while at rest. They will determine the ‘RMR’ (i.e. Resting Metabolic Rate) component within the nutrition requirements panel, as shown below.
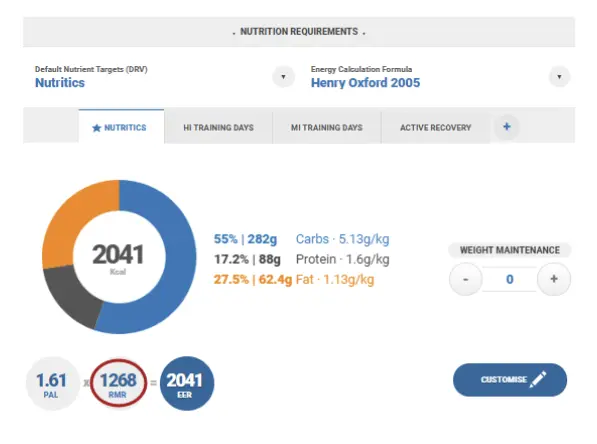
Previous research has shown that RMR can vary significantly between individuals. Known determinants of RMR include:
- Genetics, particularly race or ethnicity.
- Gender. On average, men have a greater lean mass than women.
- Age. It is known that RMR reduces with age. Research has suggested that RMR drops approximately 2% per decade.
- Exercise level. Physical activity can greatly influence body composition and weight and thus, RMR.
- Fat-free mass. If available, utilisation of your client’s fat free mass in your RMR calculations is highly advisable.
- Pregnancy.
- Clinical conditions. Chronic health conditions are known to increase a patient’s energy requirements. An accurate assessment of RMR and EER should never be conducted without the consideration of all relevant conditions.
- Some studies have also suggested that hormones such as leptin, triiodothyronine and thyroxine may also play a significant role.
While it quickly becomes clear that there are multiple factors you’ll need to consider when choosing an energy calculation formula, let’s start with the basics for now.
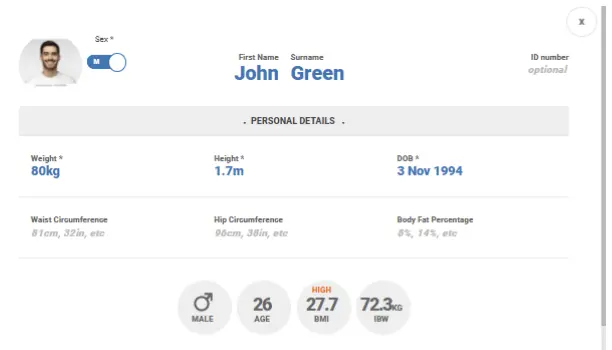
Firstly, you’ll want to determine who your client is. What do their age, weight, height and BMI look like? Our client summary tool will give you a nice overview of the aforementioned.
The total estimated energy requirement (EER) for the day is calculated using the factorial method in Nutritics. Further information on this can be found within our online tutorial guide here.
It’s worth noting that there are approximately 138 known equations for prediction of RMR. All are open to criticism, and there is much debate amongst researchers, dietitians and nutritionists regarding the most appropriate equation for use with clients and/or patients. The below is my own brief interpretation of several widely used formulae, their limitations and the patient/client base to which each formula is best suited.
As standard, we calculate RMR using the Henry Oxford equation. This is the most widely used in practice but, depending on the client you’re working with, you may wish to choose another option from the dropdown menu.
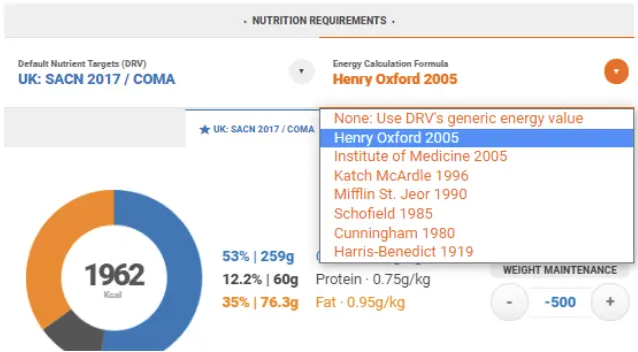
Most formulas have used large cohorts of people as the basis of their predictive analyses. Therefore, when deciding on which is most fit for your client, it is worthwhile to consider the researchers’ initial objectives while developing the equation, and the profile of the original study cohort.
Henry Oxford 2005
The Henry Oxford equation is among the ‘newer’ equations and uses weight as the primary predictor of RMR. It is thought that the Henry Oxford equation represents all ethnicities well, as it is based on 10,502 men and women (n=5794, n=4708) from both developed and developing countries.
In 2007, the British Dietetic association in their “Manual of Dietetic Practice” advised the use of this equation among modern, healthy adults and older adults. Both SACN 2011 and PENG 2011 publications also advised the use of this equation for prediction of energy requirements in healthy populations.
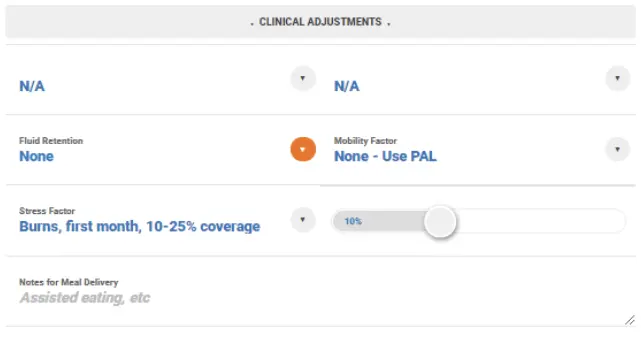
For patients who are ill, it is advisable to also apply a metabolic stress factor to account for the inflammatory response. More information on this can be found here.
Incorporation of stress factors within the EER are now available on the Nutritics health editions. Please contact support@nutritics.com if you’d like some more information around this.
The main limitation of the Henry Oxford equation is that it assumes a linear association between RMR and weight. In reality, as age increases, the association between weight and RMR decreases, meaning that this equation is perhaps less appropriate for use among overweight or older groups. It has also been shown in a number of studies to be a more accurate predictor of RMR among men than women.
Institute of Medicine 2005
Also one of the more recently developed energy equations, the Institute of Medicine equation was first published in 2002. The equations form the basis of the 2005 Dietary Guidelines for Americans.
The methodology utilised here differs from others in its approach. It does not use the factorial method (the RMR x PAL calculation you see listed in-app) and is based on experiments using doubly labelled water.
Example calculation:
Women: EER=(354-(6.91*Age))+PA*((9.36*wt)+(726*ht))
The equations were developed for both children and adults at a healthy weight with correction factors for overweight or obese individuals. This is the perhaps the most commonly critiqued aspect of the IOM derivations, as it is thought that the correction factor may lead to overestimation of energy requirements for overweight and obese individuals.
Schofield 1985
In 1985, Schofield et al. screened data from the literature dating between 1914 to 1980 and, after some fancy statistical analyses, produced predictive equations for both sexes for the following ages: 0-3, 3-10, 10-18, 18-30, 30-60 and >60 years. These went on to form the basis for the equations used in a widely cited 1985 FAO/WHO/UNU document, “Energy and Protein Requirements”.
While Schofield’s work has certainly helped in our continual strides toward more accurate and precise measurements of basal metabolic rate, more recent studies have subsequently queried the universal validity and application of these equations. The original dataset is made up of predominantly Italian subjects, a large percentage of whom were male. Growing evidence suggests that this formula has the tendency to overestimate per kilogram body weight amongst other ethnicities, particularly individuals outside of Europe.
It’s worth noting that this equation is easy to apply as it requires information on age, gender and weight only, and is still widely used in practice.
Harris-Benedict 1919 & Mifflin St. Jeor 1990
Invented in 1919 and revisited in 1984, Harris Benedict was among the earliest energy calculation equations. The formula was originally derived from a group of predominantly white individuals at a healthy weight, likely more active than the average adult is today. As the oldest of the equations still in use today, it is perhaps the most rigorously tested and validated, but still has its limitations. This formula is a more accurate predictor among men but is known to overestimate RMR between 6-15%.
Since 1990, Mifflin St. Jeor (which is essentially a modified version of the Harris Benedict equation) has become more commonly used in practice. The study sample forming the basis of the Mifflin St. Jeor method consisted of 498 normal weight, overweight, obese,and severely obese individuals ages 19 to 78 years and has been shown to perform more accurate analyses for overweight and obese individuals than other equations. Age is also incorporated within this predictive formula and this may be a useful consideration when working with older patients. It’s worth noting that the ethnicity of the group used within the Mifflin St. Jeor study sample is not known.
Katch McArdle 1996 & Cunningham 1980
Both the Katch McArdle and Cunningham equations can be utilised only if percentage body fat is known for the client in question. Ideally, the body fat percentage should be determined by bioelectrical impedance or dual energy X-ray absorptiometry.
Although it is not always feasible for clinicians to measure body fat percentage, studies consistently show that fat-free mass is the best independent predictor of RMR. These equations tend to be used most often among athletic groups and were developed with the sportsperson in mind.
In 2006, a position statement from the American Dietetic Association was released advising the use of the Cunningham equation for use amongst athletes. It was noted within this statement that the Harris Benedict equation is commonly used by sport dietitians in practice.
Summary
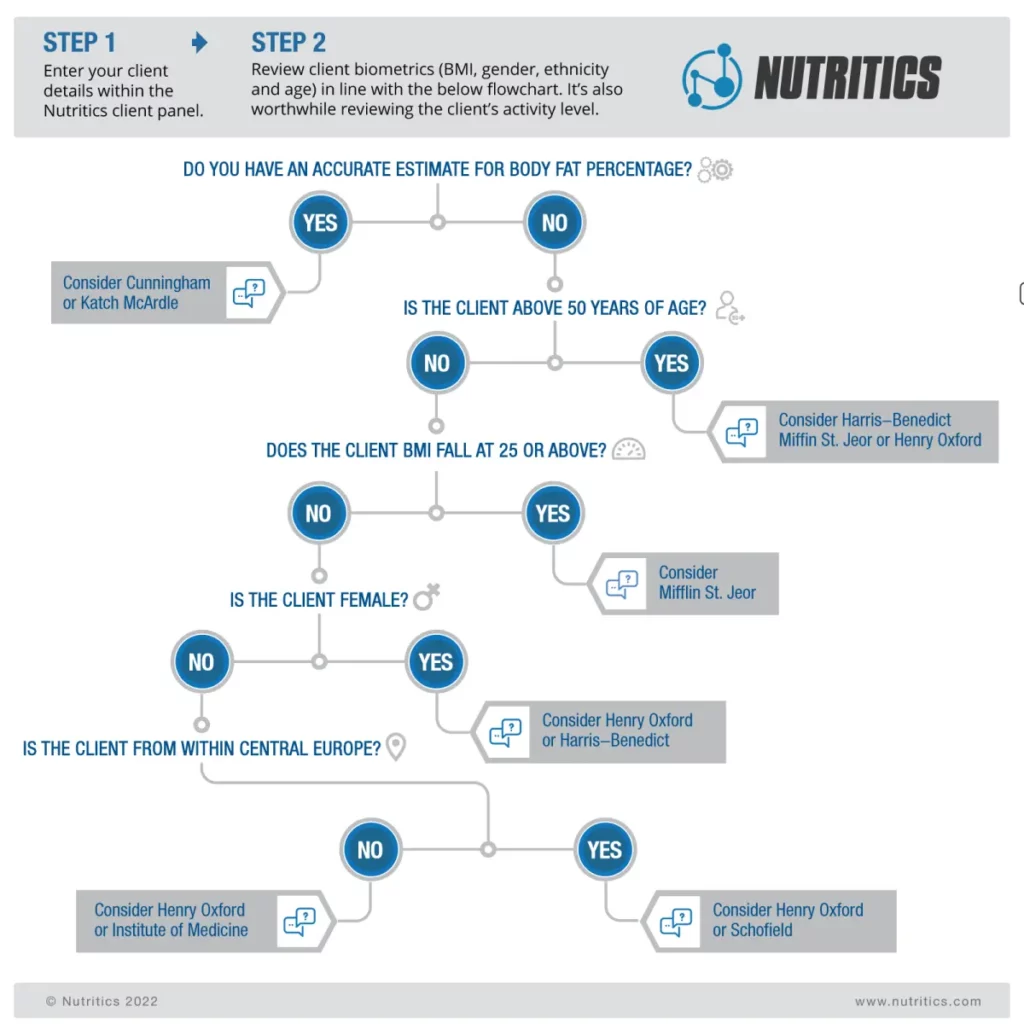
Ultimately, the equation you use to predict energy requirements should be assessed on a client by client basis, will require your best clinical judgement and should be reviewed regularly. While prediction formulae have their limitations, they are also an easy and accessible way for nutrition professionals to assess nutritional needs and align client goals alongside this. We have developed the below flowchart to help in guiding you toward an appropriate energy calculation formula for your client. Please note: this chart has been developed based on a personal interpretation of the scientific literature and should not be considered as official guidance. Client requirements can vary significantly and it is important that you take individual differences into account when assessing their needs.
REFERENCES
- Almajwal, A. M. and Abulmeaty, M. M. A. (2019) “New predictive equations for resting energy expenditure in normal to overweight and obese population,” International journal of endocrinology, 2019, p. 5727496. doi: 10.1155/2019/5727496.
- Cunningham, J. J. (1980) “A reanalysis of the factors influencing basal metabolic rate in normal adults,” The American journal of clinical nutrition, 33(11), pp. 2372–2374. doi: 10.1093/ajcn/33.11.2372.
- FAO/WHO/UNU (1985) Energy and protein requirements: Report of a jointFAO/WHO/UNU expert consultation.
- Green, A. J., Smith, P. and Whelan, K. (2008) “Estimating resting energy expenditure in patients requiring nutritional support: a survey of dietetic practice,” European journal of clinical nutrition, 62(1), pp. 150–153. doi: 10.1038/sj.ejcn.1602690.
- Harris, J. A. and Benedict, F. G. (1918) “A biometric study of human basal metabolism,” Proceedings of the National Academy of Sciences of the United States of America, 4(12), pp. 370–373. doi: 10.1073/pnas.4.12.370.
- Henry, C. J. K. (2005) “Basal metabolic rate studies in humans: measurement and development of new equations,” Public health nutrition, 8(7A), pp. 1133–1152. doi: 10.1079/phn2005801.
- Johnstone, A. M. et al. (2005) “Factors influencing variation in basal metabolic rate include fat-free mass, fat mass, age, and circulating thyroxine but not sex, circulating leptin, or triiodothyronine,” The American journal of clinical nutrition, 82(5), pp. 941–948. doi: 10.1093/ajcn/82.5.941.
- Mifflin, M. D. et al. (1990) “A new predictive equation for resting energy expenditure in healthy individuals,” The American journal of clinical nutrition, 51(2), pp. 241–247. doi: 10.1093/ajcn/51.2.241.
- Parker, E. A. et al. (2017) “Considerations when using predictive equations to estimate energy needs among older, hospitalized patients: A narrative review,” Current nutrition reports, 6(2), pp. 102–110. doi: 10.1007/s13668-017-0196-8.
- Piers, L. S. et al. (1997) “The validity of predicting the basal metabolic rate of young Australian men and women,” European journal of clinical nutrition, 51(5), pp. 333–337. doi: 10.1038/sj.ejcn.1600407.
- “Position of the American Dietetic Association, Dietitians of Canada, and the American College of Sports Medicine: Nutrition and Athletic Performance” (2009) Journal of the American Dietetic Association. doi: 10.1016/j.jada.2009.01.005.
- Sabounchi, N. S., Rahmandad, H. and Ammerman, A. (2013) “Best-fitting prediction equations for basal metabolic rate: informing obesity interventions in diverse populations,” International journal of obesity (2005) , 37(10), pp. 1364–1370. doi: 10.1038/ijo.2012.218.
- Schofield, W. N. (1985) “Predicting basal metabolic rate, new standards and review of previous work,” Human nutrition. Clinical nutrition, 39 Suppl 1, pp. 5–41. Available at: https://pubmed.ncbi.nlm.nih.gov/4044297/ (Accessed: December 20, 2021).
- Syngle, V. (2020) “Determinants of basal metabolic rate in Indian obese patients,” Obesity medicine, 17(100175), p. 100175. doi: 10.1016/j.obmed.2019.100175. Weekes, E. C. (2019) “Nutritional requirements in clinical practice,” in Gandy, J. (ed.) Manual of Dietetic Practice, British Dietetic Association. Birmingham, England: Wiley-Blackwell.
- Woodruff, S. J., Hanning, R. M. and Barr, S. I. (2009) “Energy recommendations for normal weight, overweight and obese children and adolescents: are different equations necessary?,” Obesity reviews: an official journal of the International Association for the Study of Obesity, 10(1), pp. 103–108. doi: 10.1111/j.1467-789X.2008.00525.
